Nand to Tetris is a course that teaches you how to build a computer up from nand gates
a b nand(a, b)
- - ----------
0 0 1
0 1 1
1 0 1
1 1 0
and then program Tetris for your computer. Nand game cover the first 3 projects of the course using a nice drag-and-drop interface
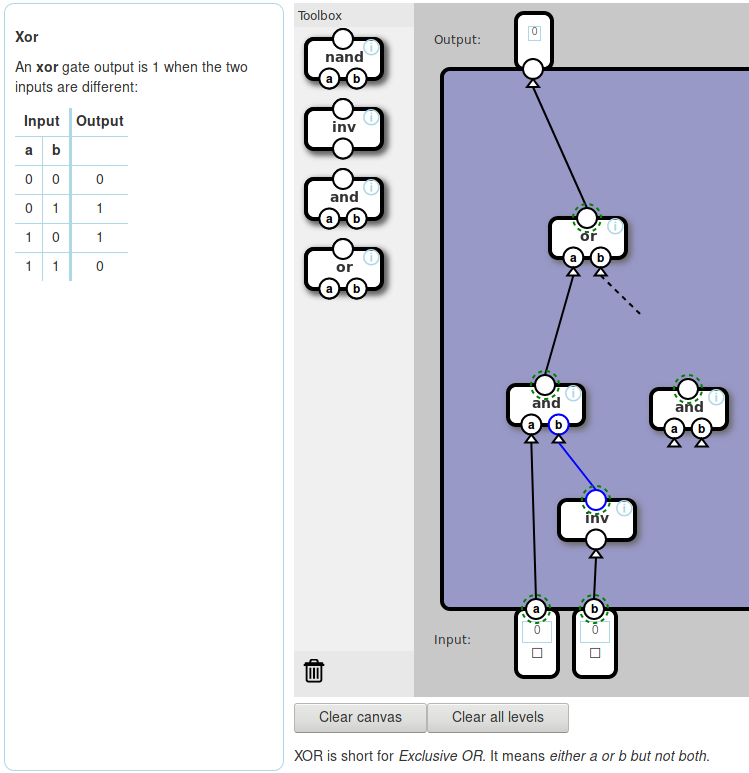
Nand game includes a number of (in my opinion) improvements to the presentation. I feel it really lets me get to the crux of the matter quickly.
This post contains solutions to Nand game and therefore Nand to Tetris. Try them first if you haven't already.
One thing I wish I could do in Nand game is to experiment with the CPU designs (rather than just implement an existing design). I quite like their interface but am much quicker (and used to) a text interface.
So I tried to preserve Nand game's simplifications to Nand to Tetris while allowing me to do just that.
I tried to come up with a language to describe the circuits I'm making. Nand to Tetris uses its own Hardware Description Language (HDL)
CHIP Xor {
IN a, b;
OUT out;
PARTS:
// Put your code here:
Not(out=notb, in=b);
Not(out=nota, in=a);
And(out=anotb, a=a, b=notb);
And(out=bnota, a=nota, b=b);
Or(out=out, a=anotb, b=bnota);
}
I'm guessing this is modelled after existing HDLs. I briefly surveyed those but think we can do better in this special case.
The slides for Nand to Tetris gives a hint for xor:
Xor(a, b) = Or(And(a, Not(b)), And(Not(a), b))
Why not just use this syntax?
Our first attempt is to use functions from an existing language, like Python.
nand = lambda a, b: not(a and b)
not_ = lambda a: nand(a, a)
and_ = lambda a, b: not_(nand(a, b))
From this point forth, we'll only use the function definition and function call features of Python and not anything builtin (like and and not used to define nand).
or_ = lambda a, b: nand(not_(a), not_(b))
xor = lambda a, b: or_(and_(a, not_(b)), and_(not_(a), b))
add1 = lambda a, b: (and_(a, b), xor(a, b))
or_3 = lambda a, b, c: or_(a, or_(b, c))
xor3 = lambda a, b, c: xor(a, xor(b, c))
add = lambda a, b, c: (or_3(and_(a, b), and_(b, c), and_(a, c)), xor3(a, b, c))
Things seem to be going pretty well and we can even test these functions.
>>> add(1, 0, 1)
(True, False)
but then we reach something like latch.
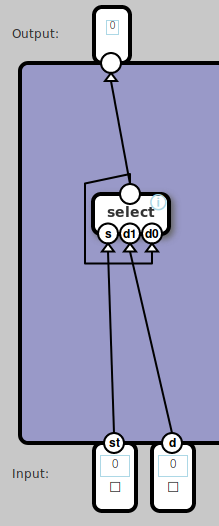
The latch is the basic component for memory and this is done by feeding its output back into itself (or rather its select gate) and I found no easy way to express that in Python.
Without the latch, we won't be able to make registers or memory.
In fact, this surfaces the timing issue we've been ignoring up to now: it takes time for signals to propagate through a gate.
not_ = lambda a: nand(a, a)
actually means the not_ gate receives input a at time t and outputs nand(a, a) at time t+1. So these aren't really equalities.
or_ = lambda a, b: nand(not_(a), not_(b))
With more nested gates, we only see a change in the output multiple time units later.
To address this, we could explicitly say what the timestamps are
or_[t+3] = lambda a, b: nand(not_(a[t]), not_(b[t]))
But it turns out that keeping the convention
The lefthand side is the value of the output at some later time t+dt when the input in the righthand side changes at time t.
is going to be enough for us. So back to latch, we could write something like.
def latch(store_mode, value):
out = select(store_mode, value, out)
return out
And this is enough to get us through to the CPU!
The syntax I ended up with is only slightly different, inspired by how the splides defined xor.
xor(a, b) = or(and(a, not(b)), and(not(a), b))
select(sel, d1, d0) = or(and(sel, d1), and(not(sel), d0))
def latch(store_mode, value) -> out:
out = select(store_mode, value, out)
Since this is a declarative definition of a circuit, I added -> for specifying the output on the same line as the inputs. This avoids defining the semantics for multiple return statements.
The essential part of the grammar for this language is
grammar = single*
single = NEWLINE | SAME_INDENT {def | inline} ('\n' | '\r')
inline = {NAME=func_name} "(" {names=inputs} ")" "=" spaces {func_calls}
func_calls! = func_call ("," spaces {func_call})*
func_call = {NAME=func_name} "(" {(argument ("," spaces {argument})* | void)=arguments} ")"
argument = hspaces {func_call | NAME=variable}
def = "def" hspacesp {NAME=func_name} "(" {names=inputs} ")"
"->" {names=outputs} ":" {body}
body! = INDENT {statement*} DEDENT
statement! = NEWLINE SAME_INDENT {names=outputs} "=" {func_call}
names! = NAME=NAME ("," {NAME=NAME})*
We can try a small program
Text instruction Bit representation
d = 3 0 000000000000011
a = d 1 11 0 001010 100 000
d = 12 0 000000000001100
d = d - 1 1 11 0 001110 010 000
if d != 0, jump to a 1 11 0 001100 000 101
load it (more on this step later)
>>> rom = [0b0000000000000011, 0b1110001010100000, 0b0000000000001100,
... 0b1110001110010000, 0b1110001100000101]
>>> rom = map(bin_list, rom)
and run
>>> cpu_cycle(cpu)
Reading rom[0]
Program counter at [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Register a is [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Register d is [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Storage instructions [[0, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1], 0]
Comparing [[0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Comparison result [0]
After running cpu_cycle(cpu) enough times, we see that it loops back, register d slowly decrement and eventually hits 0. Then it crashes since its trying to read beyond the end of rom.
Seems like a success!
The rest of this post will talk a bit about the internals of the simulator and language.
The ROM contains the list of 16-bit instructions to execute. We can implement it as RAM without write access.
rom(address) = RAM(address, 0, 0, 0)
but since the initial RAM is empty, there's no easy way to write our program into it! Before running the CPU, we manually set input values to the RAM inside the ROM but since we are going to do something by hand anyways, we may as well just use a Python function that takes an address and return the 16-bit instruction at that address.
rom = [0b0000000000000011, 0b1110001010100000, 0b0000000000001100,
0b1110001110010000, 0b1110001100000101]
rom = map(bin_list, rom)
def manual_rom(args):
(address,) = args
print "Reading rom[%s]" % parse_bin(address)
return [rom[parse_bin(address)]]
gates['manual_rom'] = FuncVertex(manual_rom, 1, 1, default=[0])
where bin_list and parse_bin convert between integers and list of bits.
Its pretty nice that we can describe a CPU using a fairly simple language. Some parts are still a bit tedious if written by hand.
Right now, applying not (or and) to 16 bits needs lots of repetition.
def not16(bits) -> out:
bit15, bit14, bit13, bit12, bit11, bit10, bit9, bit8, bit7, bit6, bit5, bit4, bit3, bit2, bit1, bit0 = unpack(bits)
out = pack(out15, out14, out13, out12, out11, out10, out9, out8, out7, out6, out5, out4, out3, out2, out1, out0)
out0 = not(bit0)
out1 = not(bit1)
out2 = not(bit2)
out3 = not(bit3)
out4 = not(bit4)
out5 = not(bit5)
out6 = not(bit6)
out7 = not(bit7)
out8 = not(bit8)
out9 = not(bit9)
out10 = not(bit10)
out11 = not(bit11)
out12 = not(bit12)
out13 = not(bit13)
out14 = not(bit14)
out15 = not(bit15)
There could be some language features added to help with this. The question is which one?
For the moment, some of the inputs and outputs are lists of bits instead of single bits. The intended interpretation is that everything should be flattened in an actual circuit. For example, an input of
[[1, 0, 1], [1, 1, 1, 1], 0]
should really be
[1, 0, 1, 1, 1, 1, 1, 0]
If enough language feature is added to get the same results, pack* and unpack* won't be needed anymore.
Although I have to say this does serve as a bit of an invariant check at the moment which catches misaligned bits.
Related to this, it'd be useful to be able to address a single bit within a group (like bits[15]) instead of having to unpack them first (bit15, bit14, ..., = bits).
Currently this CPU has 2 slots for RAM addressed by 1 bit. It could be increased to 2^14 like in Nand to Tetris or even 2^14. Its possible but still tedious. For example for 3-bits RAM, we could write.
and3(a, b, c) = and(a, and(b, c))
def RAM3(address, store_mode, bits, clock) -> regaaa:
a2, a1, a0 = unpack3(address)
n2 = not(a2)
n1 = not(a1)
n0 = not(a0)
reg000mode = switch(and3(n2, n1, n0))
reg001mode = switch(and3(n2, n1, a0))
reg010mode = switch(and3(n2, a1, n0))
reg011mode = switch(and3(n2, a1, a0))
reg100mode = switch(and3(a2, n1, n0))
reg101mode = switch(and3(a2, n1, a0))
reg110mode = switch(and3(a2, a1, n0))
reg111mode = switch(and3(a2, a1, a0))
reg000 = register16(reg000mode, bits, clock)
reg001 = register16(reg001mode, bits, clock)
reg010 = register16(reg010mode, bits, clock)
reg011 = register16(reg011mode, bits, clock)
reg100 = register16(reg100mode, bits, clock)
reg101 = register16(reg101mode, bits, clock)
reg110 = register16(reg110mode, bits, clock)
reg111 = register16(reg111mode, bits, clock)
reg11a = select16(a2, reg111, reg110)
reg10a = select16(a2, reg101, reg100)
reg01a = select16(a2, reg011, reg010)
reg00a = select16(a2, reg001, reg000)
reg1aa = select16(a1, reg11a, reg10a)
reg0aa = select16(a1, reg01a, reg00a)
regaaa = select16(a0, reg1aa, reg0aa)
Nand to Tetris suggests making 6-bits RAM from 3-bits RAM and so on from this point. With loops, this could be much easier. Its not clear to me how powerful the loops would need to be.
Right now, all component outputs are cached which means a gate's output is calculated only when at least one of its inputs changes. But for constants like zero_1() and zero_16() (needed since the number of bits for that input isn't easy to deduce), the functions are never evaluated. This in turn means what they feed into always gets the default None input.
As an ugly hack, these constant gates are given an arbitary input from its component, which is then ignored. A better idea to patch up the caching mechanism is needed. This might be affected by what's done for packing/unpacking.
We could consider things like removing commas since they aren't really needed except for visual separation but spaces could do just as well.
Despite all this, it was surprising to me that you could pack all the information need to go from nand gates to CPU in about 220 lines of text that's pretty readable.
With the language and simulator in place, now I can go and try out different CPU designs.
The source for the parser and simulator is available here. The CPU described in this language is here.
Images used are from the public domain. Nand gate
Posted on Sep 27, 2018