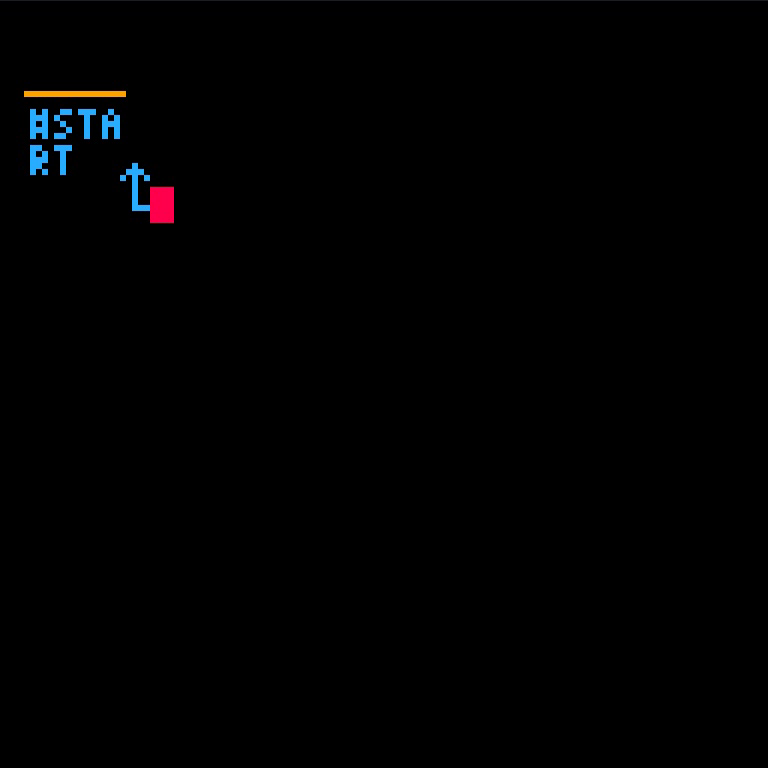
Just-in-time programming is a workflow for creating a program top-down, while a program is running. This is typical in Smalltalk environments like Squeak.
In this post, I want to describe an instruction level variant of this.
I think the best way to describe instruction level just-in-time programming (IL-JIT programming) is by showing how it works. I'll start with the classic Fibonacci example (Rosetta code has many implementations). We'll implement Fibonacci while evaluating fib(3).
The example that follow are in a concatenative language that is a simplified version of FlpcForth. The main things to know are that it has
And all functions are formally nullary, but have an implicit arity defined by how many elements they remove from the top of the global parameters stack. Their return value are pushed to the top of this stack.
Here's the whole video of the implementation that we'll go through step-by-step. Click on it to play.
Memory is displayed left to right, wrapping around to the next row. Each memory cell holds either a function, string or label (that executes as a no-op). The input stack is drawn above the program counter. Only the top of the call stack is shown.
Each time we write an instruction, the program counter takes a step. We can also advance the program counter without writing any instruction.
Starting with the empty program,
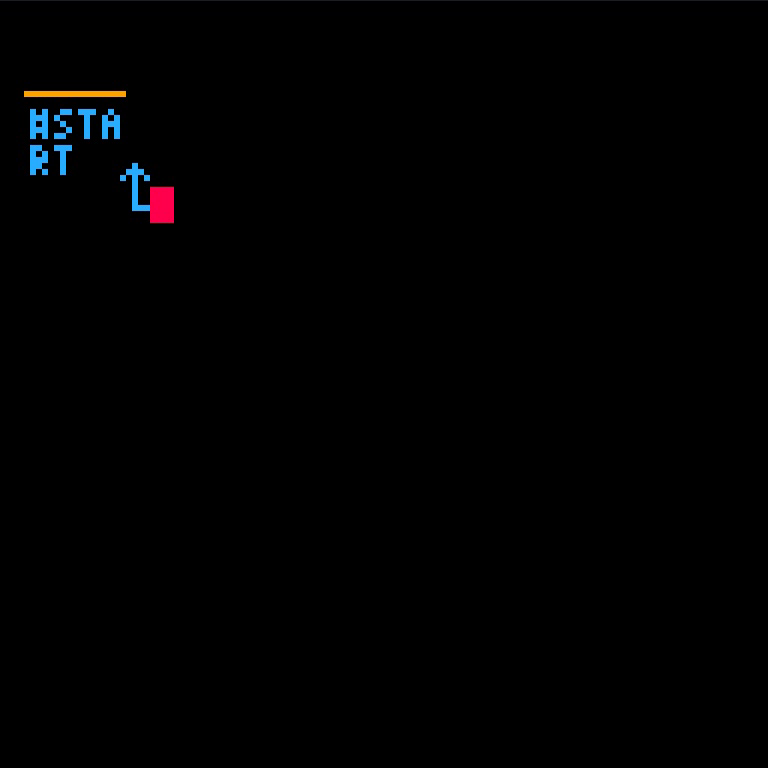
we'll call the fib function with argument 3
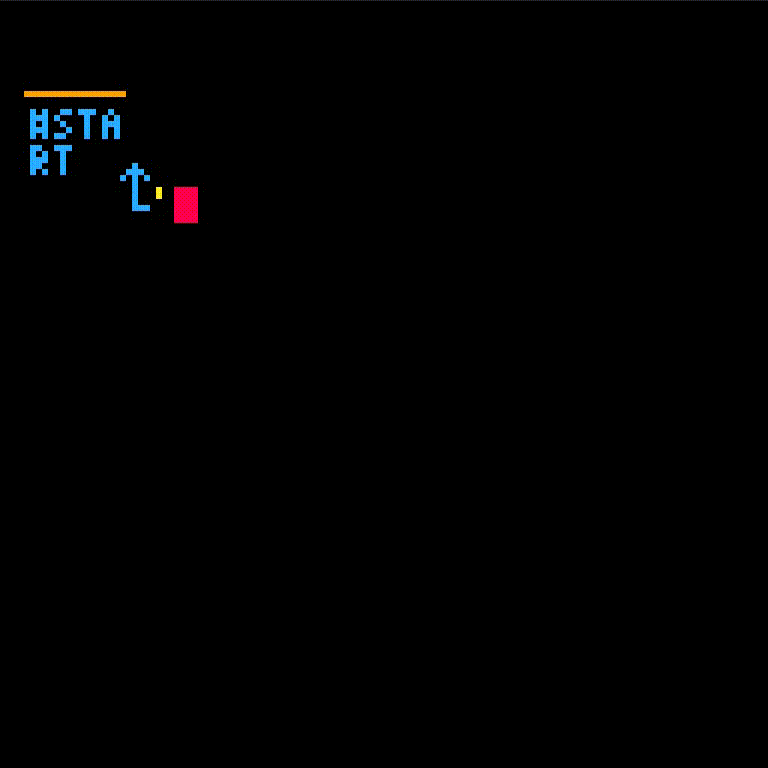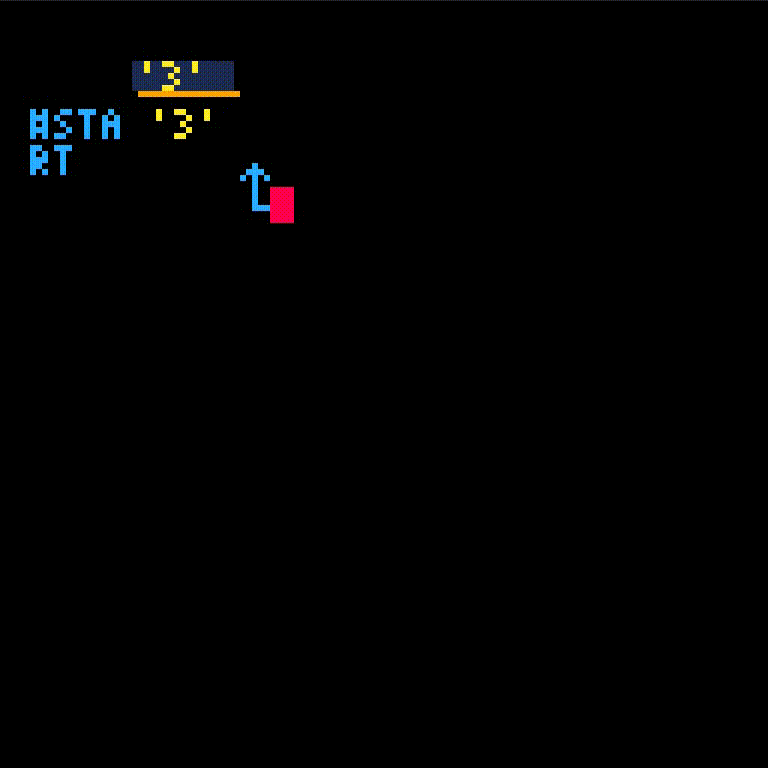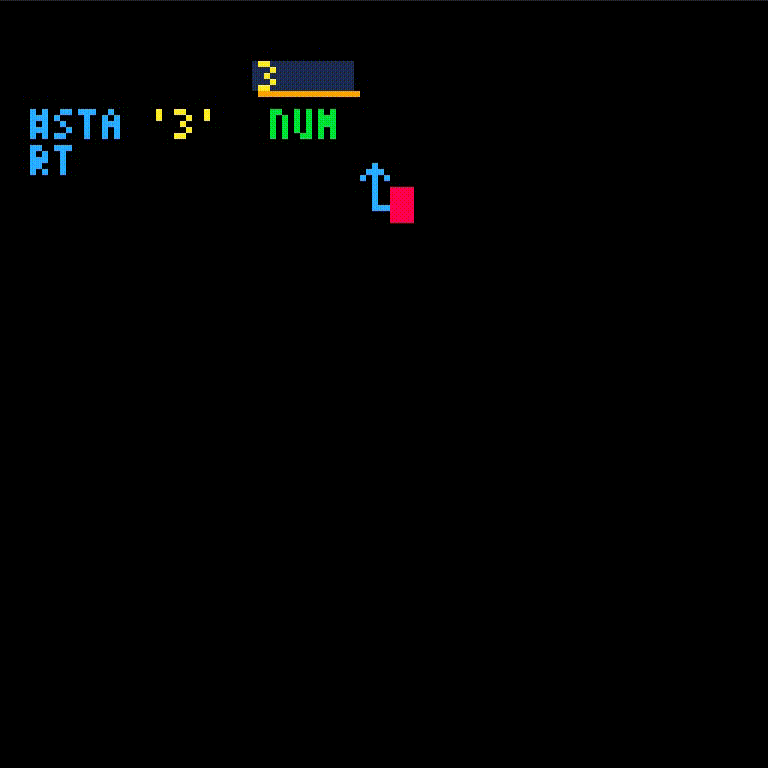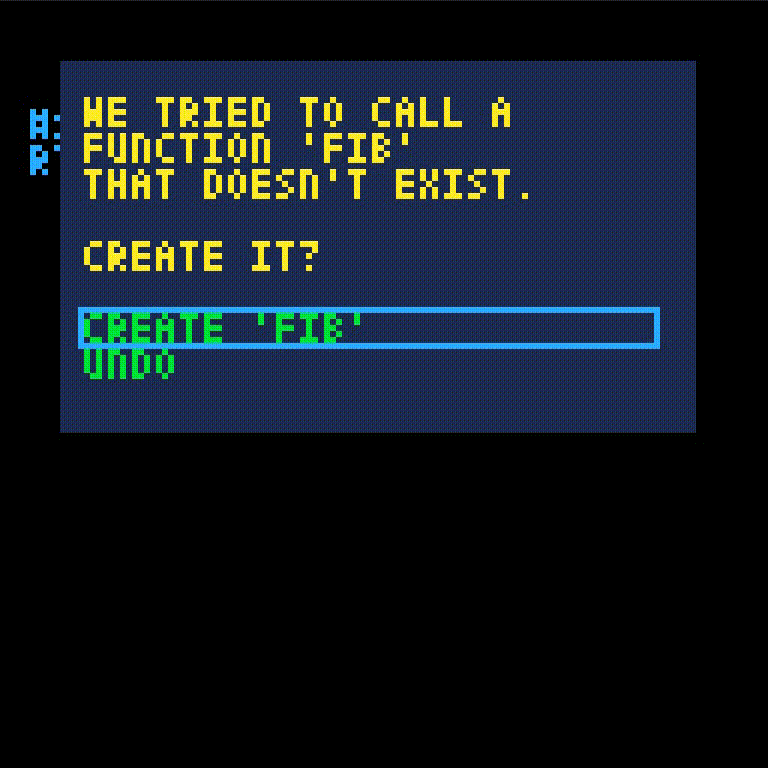
fib isn't defined yet which gives an error. We'll create fib and retry the call.
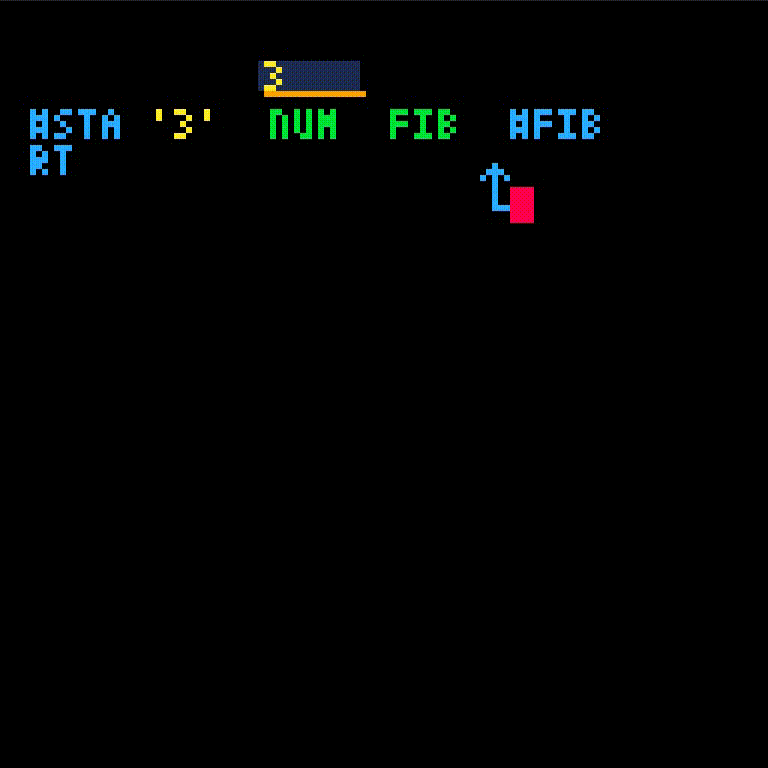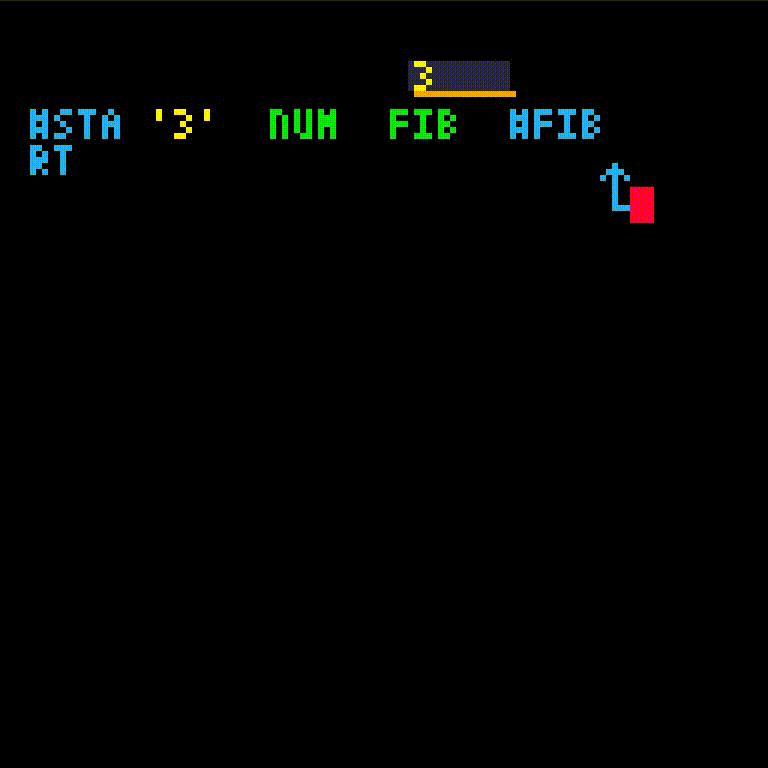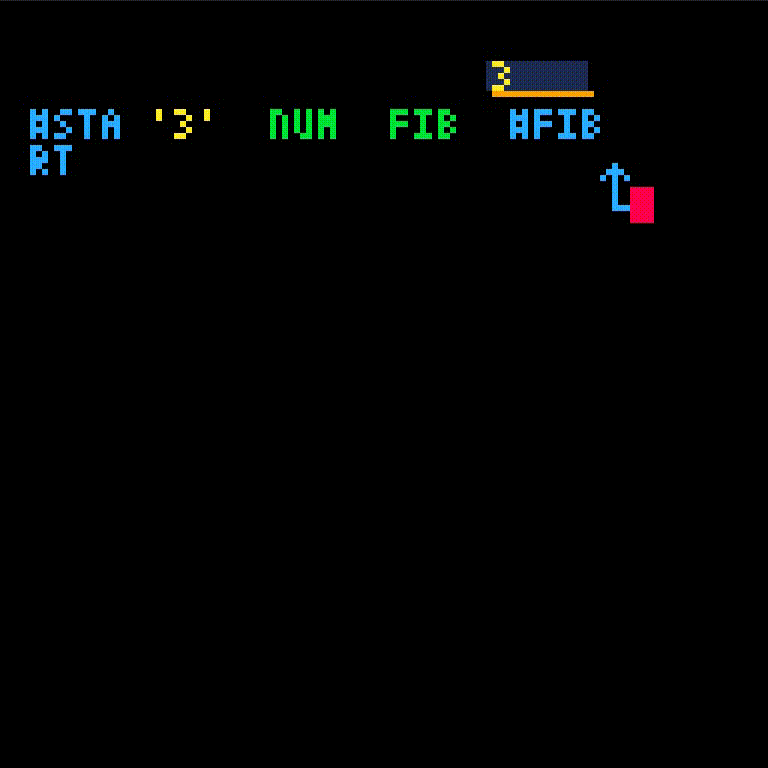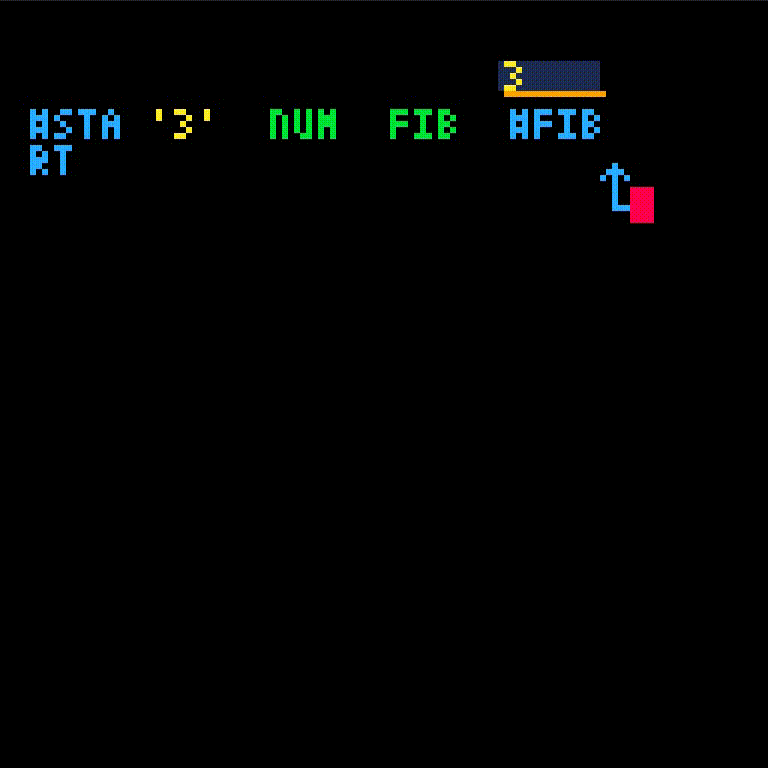
fib will take one argument, which we'll name i.

Normally, we may want to check for some base case. However, since we have the argument 3 in hand, let's only write the i > 2 case for now.
We should return fib(i - 2) + fib(i - 1). Compute the first part fib(i - 2).
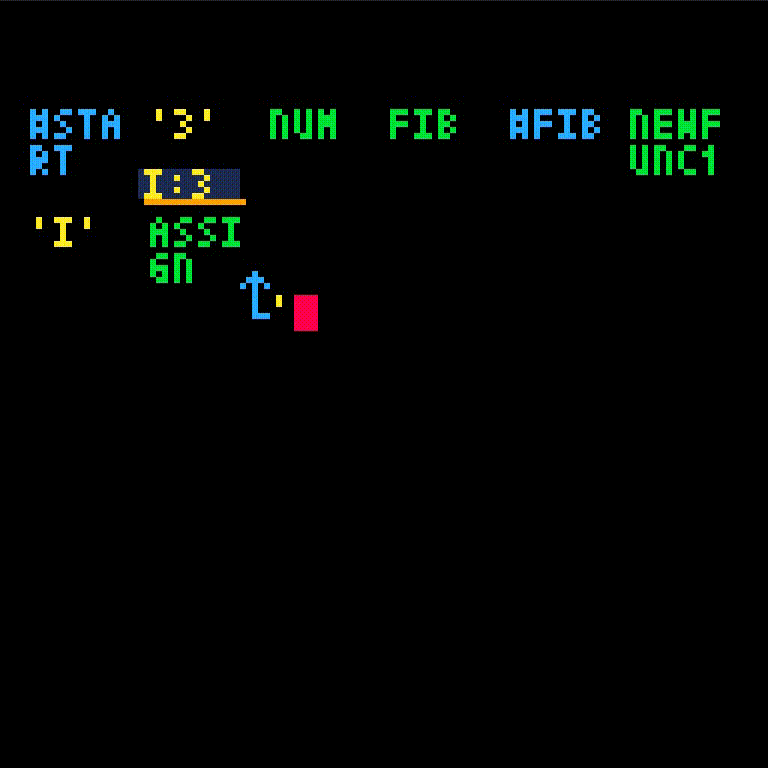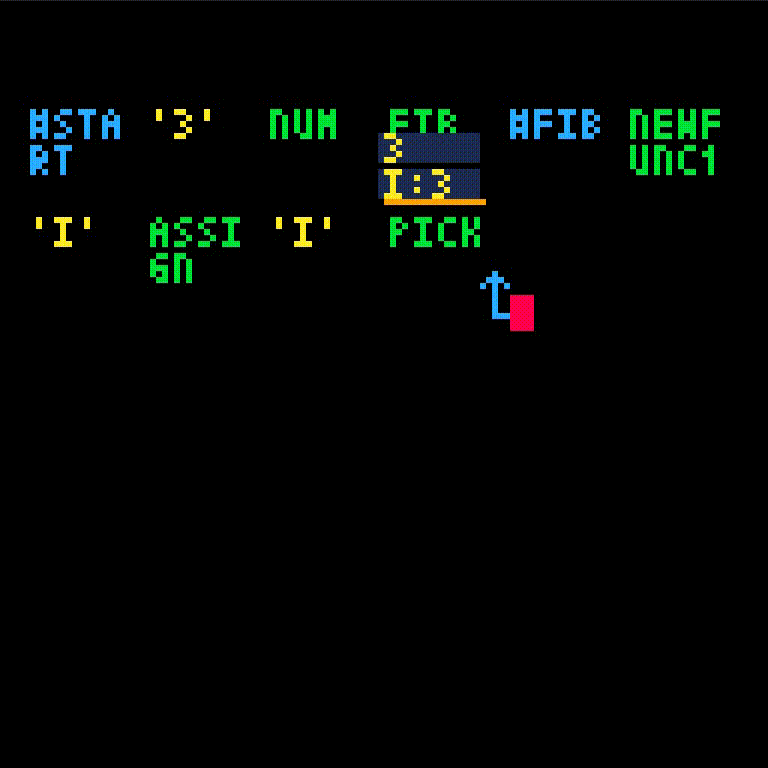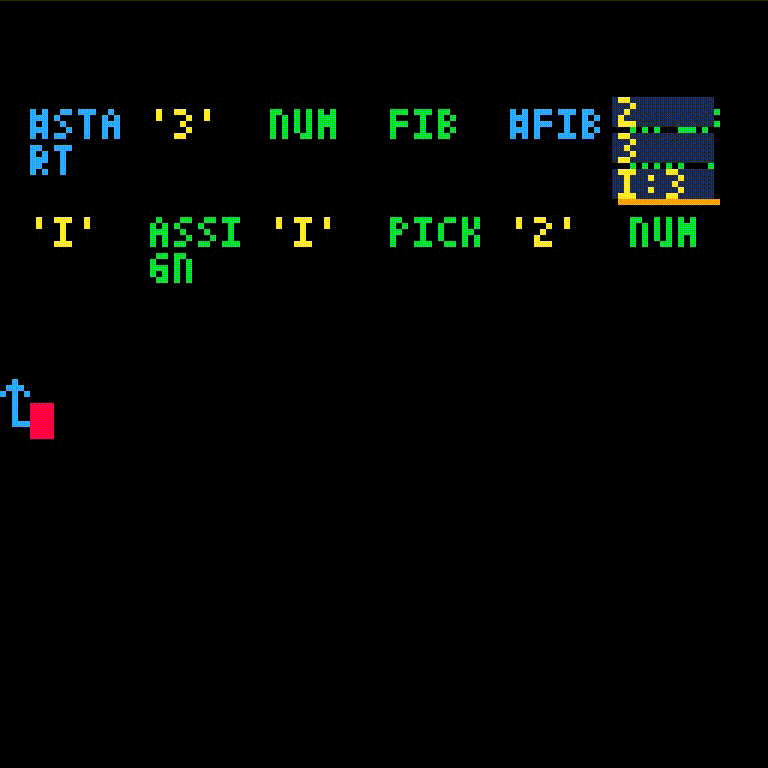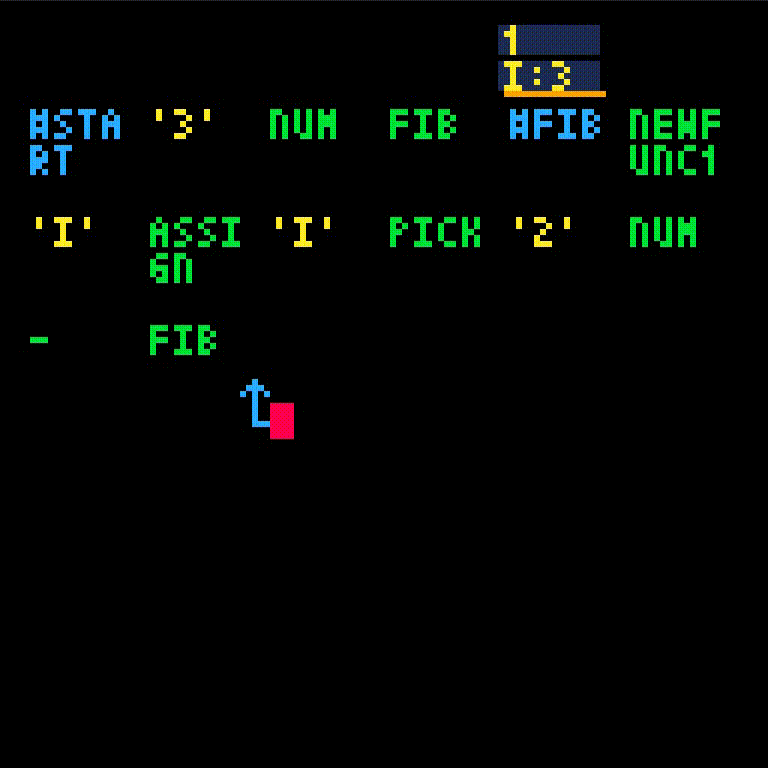
Since this calls fib recursively, let us follow the execution. First, we manually let a few instructions execute

until we need to intervene. In this recursive call i = 1 so we do need the base case now.

Like for fib, 'base' refers to a function that doesn't exist yet. As before, create the function and call it again.
When i < 3, we'll just return 1 so that is what base will do.

Now that we've evaluated fib(3 - 2), we can evaluate fib(3 - 1).

and let it run for a bit.

Now add the result and return it.

We got 2, which is the right result.
Typical JIT programming restarts frames on error. That is, it unwinds a number of frames (decided by the user). For example, if we called f1 which called f2 which called f3 which called f4, the stack will look like
f4(x)
f3(x)
f2(x)
f1(x)
Then we rewind it to, say, just
f1(x)
and we call f2(x) again [side-effects].
With instruction level JIT programming, no stack in unwound and in fact, most of the time, nothing is undone. The instruction counter is merely paused until it is asked to step again. Even for missing function, we could pause, wait for the function to be created and attempt to call it again.
Though I think IL JIT programming would benefit from being supplemented with frame restarts, for when larger chunks of code needs to be corrected.
Some advantages of either kind of JIT programming
I think I could get something like this to work for Flpc, even writing in the high level FlpcPython language. Here's how it would work.
if ... : or repeat: block), an anonymous fixed size empty function is added to memory and a pointer to it written as part of the body of the caller.Here's what the code and memory may look like, following the same Fibonacci example as before.
At first the code looks like
fib <- fun[i]:
fib(i - 2)
and memory looks like
names dict: fib -> 100
memory: <assign:> <str i> <prim pushi:> <int 2> <prim -> <mem 100 fib>
address: 100 101 102 103 104 105
We run the program for a bit and after fib is called a second time we insert base case checking
fib <- fun[i]:
if i < 3:
fib(i - 2)
names dict: fib -> 100
memory: <newfunc1> <assign:> <str i> <prim pushi:> <int 3> <prim <> <mem 200 anonymous> <prim if>
address: 100 101 102 103 104 105 106 107
memory: <prim pushi:> <int 2> <prim -> <mem 100 fib>
address: 108 109 110 111
memory: [...] <prim breakpoint> <prim breakpoint> <prim breakpoint>
address: [...] 200 201 202
and once the program counter reaches the inside of the if block, we add
fib <- fun[i]:
if i < 3:
return(1)
fib(i - 2)
names dict: fib -> 100
memory: <newfunc1> <assign:> <str i> <prim pushi:> <prim 3> <prim <> <mem 200 anonymous> <prim if>
address: 100 101 102 103 104 105 106 107
memory: <prim pushi:> <int 2> <prim -> <mem 100 fib>
address: 108 109 110 111
memory: [...] <prim pushi:> <int 1> <prim return>
address: [...] 200 201 202
After we return from the recursive call, we can add the rest of the function body.
fib <- fun[i]:
if i < 3:
return(1)
fib(i - 2) + fib(i - 1)
return()
names dict: fib -> 100
memory: <newfunc1> <assign:> <str i> <prim pushi:> <prim 3> <prim <> <mem 200 anonymous> <prim if>
address: 100 101 102 103 104 105 106 107
memory: <prim pushi:> <int 2> <prim -> <mem 100 fib>
address: 108 109 110 111
memory: <prim pushi:> <int 1> <prim -> <mem 100 fib> <prim +> <prim return>
address: 112 113 114 115 116 117
memory: [...] <prim pushi:> <int 1> <prim return>
address: [...] 200 201 202
This design seems to work but I don't know if I will add it to Flpc yet.
I didn't find any canonical name for the workflow used in Squeak Smalltalk so I called it JIT programming here. There's a C2 wiki page that named it this as well. Some other possible names: top-down programming, incremental programming.
[side-effects] If some functions already performed side-effects like reading from a file or a network request then these are not undone and the program may end up in an inconsistent state. In this case, more needs to be restarted, up to the entire program.
However, we can usually locally (i.e., on a per functionality basis) separate side-effects from pure or "pure enough" functions. And then only restart on the pure portions (or a larger groups that reperform all side-effects). This separation is something you might want in your code anyways
Posted on May 6, 2021